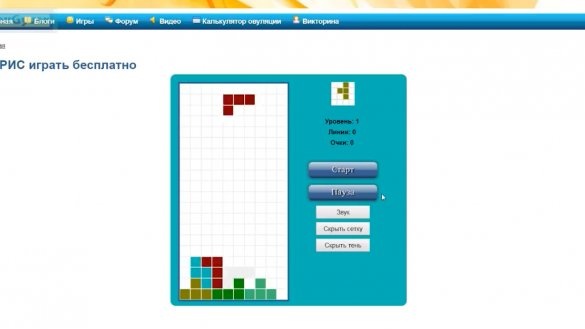
Šodien mēs izpētīsim Tetris spēles iekšpusi, kas rakstīta zem platformas arduino un LED matrica.
Šī pašdarinātā produkta autors ir AlexGyver, tāda paša nosaukuma YouTube kanāla autors. Laipni lūdzam brīnišķīgajā kvadrātpikseļu pasaulē.
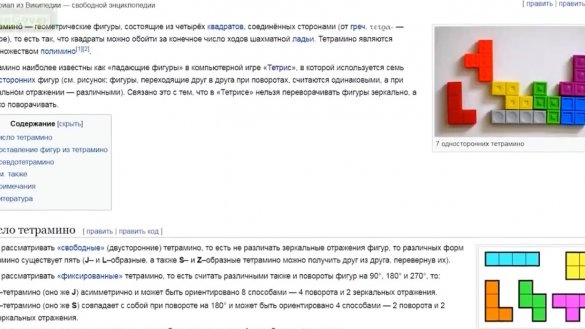
Sāksim ar stāstu. Tetris ir spēle, kurā skaitļi, kas sastāv no 4 kvadrātiem, krīt no augšas uz leju. Dažādās kombinācijās šīs formas var pagriezt un pārvietot pa kreisi un pa labi. Spēles mērķis ir savākt horizontālos līmeņus, kas tiek notīrīti, un punkti jums tiek piešķirti. Zaudēšana tiek uzskatīta par brīdi, kad jaunajam skaitlim vairs nav kur krist. Tetris izgudroja padomju programmētājs Aleksejs Leonidovičs Pažitnovs.
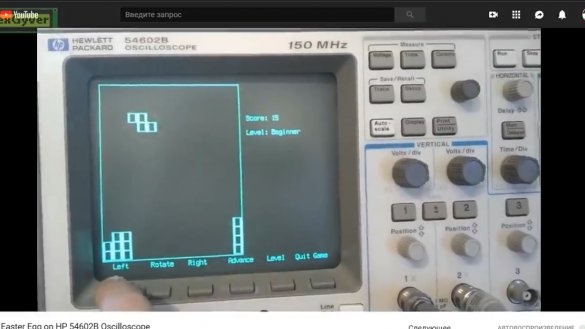
Sākotnējā Pascal versija parādījās 1984. gada 6. jūnijā. Kopš tā laika Tetris ir nogājis garu ceļu un ir pārnests uz visām platformām, kurās parasti ir iespējams spēlēt spēles, kā arī uz ierīcēm, kas vispār nav paredzētas spēlēm, piemēram, piemēram, inženierijas kalkulators, osciloskops un, neticēsit, lodāmurs.
Pēc pārdoto komerciālo versiju skaita Tetris ir pārāks par jebkuru citu spēli cilvēces vēsturē. Tikai vienam Game Boy tika pārdoti 35 miljoni eksemplāru, nemaz nerunājot par portatīvo Brick Game, kas gandrīz visiem bija vienā reizē.
Mēs sāksim tetris uz arduino un krāsu matricas ieviešanu ar “kruķu” analīzi. Matricu veido trīs krāsu adreses gaismas diodes. Šāda veida matricas problēma ir tā, ka tā ir pārāk forša. Katra pikseļa krāsa ir kodēta ar 24 bitiem, tas ir, 8 bitiem katram komponentam: sarkana, zaļa un zila. Par arduino šāda veida datu nav, ir šādi - 32 biti.
Visu gaismas diožu krāsas jāsaglabā RAM, jo mēs tās mainīsim. Turklāt matricai no 16 līdz 16 mums ir tieši 1 KB aizņemtas dinamiskās atmiņas, un arduino nano ir tikai 2 no tām.
Pievienojiet vēl dažas bibliotēkas un sāciet rakstīt kodu, atmiņa beigsies. Autore pamatā neizmanto, piemēram, arduino mega, kur ir vairāk atmiņas. Mērķis ir padarīt spēli arduino nano, izmantojot vienkāršus, standarta un labi zināmus rīkus, bet tajā pašā laikā nestandarta pieejas un “kruķus” un ar viņu palīdzību panākot optimālāko kodu.
Pirmais “kruķis” būs atteikšanās atsevišķi glabāt atmiņā figūru pozīcijas un kopumā visu, kas notiek uz ekrāna.Mums jāuzglabā barošanas figūras punktu koordinātas un jau izkritušo figūru punktu koordinātas, tas ir, maksimums, mums ir nepieciešams vēl 1 masīvs, divdimensiju 16 pa 16, un tas ir tik daudz, cik 256 baiti.
Jums un man jau ir visu pikseļu krāsu klāsts, izmantosim to. Patiešām, papildus tam, ka mēs varam ievietot krāsainu punktu uz matricas, mēs varam izmērīt esoša punkta gaismu, lai mēs strādātu ar krāsām.
Tetris sākas ar krītošu bloku, kuru kontrolē ar pogām un matricas koordinātu sistēmā ir 2 koordinātas. Tas ir ļoti vienkārši, mēs izveidojam taimeri, saskaņā ar kuru bloks samazināsies. Šī ir autora bibliotēka, jūs varat lasīt vietnē.
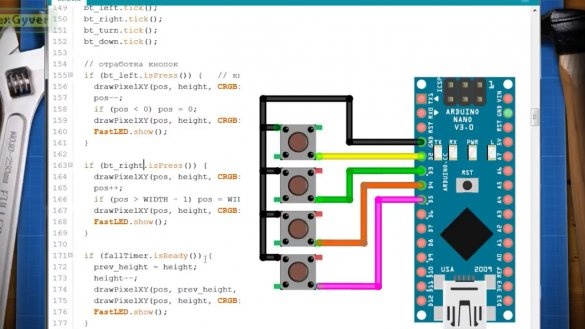
Lai apstrādātu pogas, autors izmanto arī savu bibliotēku. Pogu savienošanas shēma ir smieklīgi vienkārša: 4 pogas, 8 vadi.
Katrā taimera solī mēs uzzīmējam punktu pikseļu zem vecā un veco punktu uzzīmējam melnā krāsā, tas ir, izslēdziet gaismas diodi. Noklikšķinot uz pogas, mēs darām to pašu, bet ar horizontālu koordinātu. Nu, pieklājībai, mēs ierobežosim matricas lielumu, lai punkts nepārsniegtu lauku.
Redziet, nekas sarežģīts. Bet tas nenotiek ilgi, jo ir pienācis laiks zīmēt skaitļus. Mēs strādāsim šādi: mēs saglabāsim atsauci uz piegādes punktu, par kuru mēs jau esam uzrakstījuši, mēs to sauksim par galveno punktu vai galveno bloku. Galvenais bloks pārvietojas matricas koordinātu sistēmā, mēs to jau esam izdarījuši. Visas Tetris figūras sastāv no 4 blokiem, tāpēc, starp citu, to sauc par Tetris.
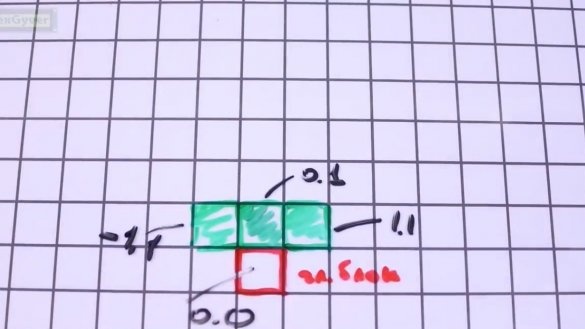
Attiecīgi mums atliek pabeigt vēl 3 bloku pievienošanu galvenajam blokam. Uzrakstīsim viņu koordinātas galvenā bloka koordinātu sistēmā, lai galvenais bloks vienmēr būtu zemāk. Tas ir ļoti vienkārši, ņemt apgrieztā burta T. skaitli. Galvenajam blokam no apakšas uz centru koordinātu sistēmā ir koordinātas 0,0.
Augšējais bloks ir 0,1, labais ir 1,1 un kreisais ir -1,1.
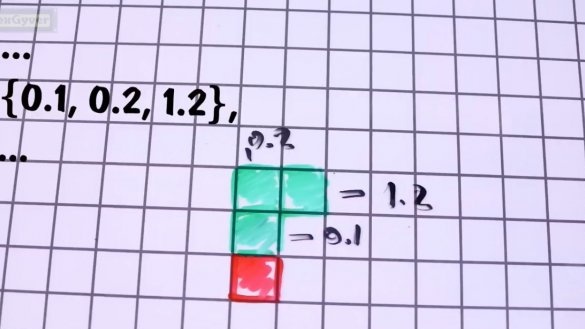
Paņemiet burtu G. Apakšējais ieraksts ir 0,0, nākamais 0,1, nākamais 0,2 un 1.2. Burta mala.
Mēs ierakstām šīs koordinātas masīvā šādā formā: {0,1, 0,2, 1,2} un nometiet masīvu zibatmiņā, lai netērētu dinamisko atmiņu. Kas attiecas uz figūru rotāciju. Skaitļus pagriezt nav iespējams. Tas ir vārgs, tāpēc ir ļoti grūti izskaidrot mikrokontrolleram, kā to izdarīt. Lai to izdarītu, jums jāiestata rotācijas centrs, kaut kā sadaliet figūru daļās un katrai daļai jāmeklē jaunas koordinātas, ņemot vērā spēcīgu pikselēšanu, kas acīmredzami novedīs pie kļūdām, un tas izrādīsies muļķības. Problēma tiek atrisināta ļoti vienkārši, mums atmiņā paliks visas 4 pozīcijas visiem skaitļiem un visiem.
Patiesībā tagad atliek nejauši izvēlēties skaitļa numuru un uzzīmēt to ap krītošo bloku. Šeit visiem 3 atlikušajiem blokiem mēs ņemam koordinātas no zibatmiņas, pārtulkojam tās matricas globālajās koordinātēs un ieslēdzam gaismas diodes. Starp citu, krāsa tiek izvēlēta arī nejauši no 6 vienkāršākajām un spilgtākajām rgb telpas krāsām. Arī figūras rotācijas leņķis kārtas sākumā tiek iestatīts nejauši, un, nospiežot pogu uz augšu, ņemiet tikai nākamo koordinātu komplektu, lai to noformētu un pagrieztu pulksteņrādītāja virzienā. Formas pārvietošana darbojas vienādi. Pirmkārt, mēs izdzēšam skaitli iepriekšējā pozīcijā, tas ir, zīmējam to melnā krāsā, tad jaunajā pozīcijā uzzīmējam pašreizējo figūras krāsu. Griežoties atkal, mēs izdzēšam veco pozīciju un vienkārši uzzīmējam jaunu.
Programmaparatūru var lejupielādēt vietnē. Mēs analizēsim tikai būtību. Sāksim ar kreisās un labās sienas un apakšas pārbaudi. Ar dibenu viss ir ļoti vienkārši, mēs skatāmies uz katru kritiena soli, vai bāzes vienība ir sasniegusi 0 augstumu, tas nav grūti, taču katru reizi, kad nospiežam vadības pogu, mums jāredz, vai figūras galējais punkts ir pieskāries matricas sānu sienām.
Ja pieskaras, nepārvietojiet figūru. Tas pats attiecas uz figūru rotāciju. Piemēram, ja figūras jaunā pozīcija pārsniedz sienas, tad rotācija ir aizliegta, un tā kā visi figūriņas mums ir dažādas formas, tad visi galējie bloki ir atšķirīgi. Katram skaitlim būtu iespējams krāsot atsevišķus galējus blokus, lai vienkāršotu mikrokontrollera darbu, taču ļaujiet uzskatīt, ka viņi to izgudroja.
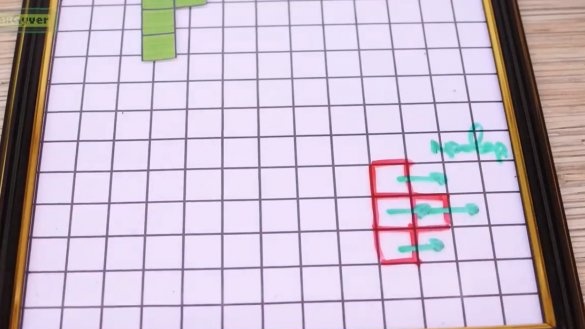
Viss ir ļoti vienkārši. Bet nākamais uzdevums ir daudz interesantāks. Mums jāpārbauda, vai nav sadursmju ar blokiem, kas jau atrodas zemāk.Ja mums būtu masīvs, kurā būtu visu lauka elementu stāvoklis, tas būtu vienkāršāk, taču lentes pikseļiem mēs izmantosim krāsu masīvu, tāpēc mums būs stilīgākais “kruķis”. Kāda ir faktiskā problēma? Šķiet, ka viss ir vienkārši, nokrīt zaļa figūra, un katru kritiena soli, katru nobīdi uz sāniem un katru mēģinājumu pagriezties vajadzētu pārbaudīt, vai figūra jaunajā stāvoklī balstās uz jau guļošajām figūrām. Ja visiem blokiem apkārtējā krāsa ir vienāda ar melnu vai vienāda ar figūras krāsu, tad mēs pieļaujam kustību vēlamajā virzienā. Tas darbosies, kamēr forma, kas atrodas zem mums, ir tādā pašā krāsā kā krītošā forma. Tas faktiski ir “kruķis”: kritušo formu pārkrāsosim citā krāsā. Pārkrāso acīm nemanāmi, bet programmai to labi pamana. Jums atliek tikai nedaudz palielināt pašreizējās formas krāsas spilgtumu, un tas arī viss.
Skaitlis nokrita uz dibena vai cita figūra, tā spilgtums manāmi nepieauga, un jaunajā kārtā krītošie skaitļi vairs nesajauks tās krāsu ar savējiem, tie kritīs uz tā un tiks fiksēti tādā pašā veidā, nedaudz pievienojot spilgtumu.
Starp citu, nospiežot pogu uz leju, skaitlis lielā ātrumā metas lejā un ieņem savu vietu.
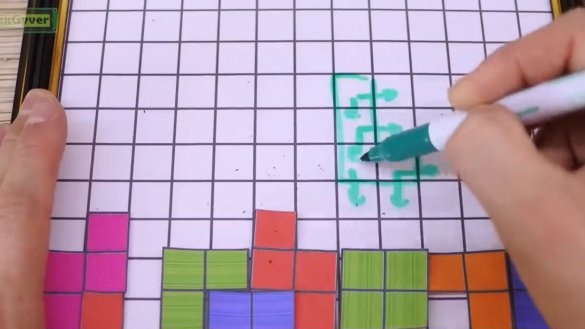
Mūsu Tetris ir palicis pēdējais, proti, piepildīto līmeņu pārbaude un notīrīšana horizontāli. Šeit viss ir vienkārši. Pēc figūras fiksēšanas kārtējā kārtā mēs virzāmies pa līnijām un salīdzinām pikseļu krāsas ar melnu. Ja visā rindā nav neviena melna pikseļa, mēs notīrīsim visu līniju.
Atklātās līnijas tiek aizpildītas ar baltu krāsu, pēc tam spilgtums pakāpeniski pazeminās līdz nullei un tiek iegūta animācija. Turklāt visi pikseļi, sākot no pirmās aizpildītās līnijas līdz augšai, tiek nobīdīti uz leju un nodzēsto līniju skaits. Šo procesu atkārto, līdz nav pabeigtu līmeņu. Mēs arī pārbaudām, vai esam sasnieguši virsotni, kas nozīmē zaudēt. Šajā gadījumā tiek parādīts konts, kas vienāds ar dzēsto līmeņu skaitu.
Konts tiek parādīts skaitļos, kas atmiņā tiek saglabāti kā skaitlis un nulle, pēc kuriem gaismas diodes tiek ieslēgtas vai izslēgtas. Tas izskatās adrešu matricā rakstītais Tetris. Paldies par uzmanību. Tiekamies drīz!
Video: