Atzīmējiet priekšējo plāksni. Universāls mērogs.
1. daļa. Kāpēc “universāla” skala?
Man bija vajadzība sadalīt apaļo sagatavi 7 daļās. Es mēģināju sadalīt 360 ar 7. Tātad, ko? Nav sadalīts bez pēdām! Un uzreiz jautājums: kā man var palīdzēt mērogs uz plāksnītes, kas iezīmēts 360 daļās? dalījums pa vienu grādu? Atbilde: nekādā veidā.
Tāpēc radās ideja apzīmēt plāksnīti, uz tās uzliekot universālu skalu. Ideja ir ievietot vēl 4 svarus galvenajā skalā.
Galvenā skala, sauksim to, ir priekšējās plāksnes izkārtojums 15 grādu leņķī. Uz plāksnītes mēs izgatavojam atzīmes "0", "90", "180" un "270". Tad katras zīmes abās pusēs mēs riskējam ar atšķirīgām dalījuma vērtībām. Tātad sektorā no 330 līdz 30 grādiem (“0” vai “360” pa vidu) mēs izkārtosim 60 dalījumu skalu, t.i. viens dalījums būs vienāds ar 6 grādiem.
Sektorā no 60 līdz 120 grādiem (“90” vidū) novietojiet skalu ar 48 dalījumiem, t.i. viens dalījums būs vienāds ar 7,5 grādiem.
Seguma plāksnes sektorā no 150 līdz 210 grādiem (“180” vidū) atzīmējam skalu ar 42 dalījumiem, tas ir, vienas dalīšanas cena ir 8,75 grādi.
Seguma plāksnes sektorā no 240 līdz 300 grādiem (“270” vidū) mēs novietosim 36 dalījumu skalu, t.i. ar dalīšanas cenu 10 grādi.
Un tagad ir maz argumentu par labu šādai plāksnes sadalīšanai.
1. Izmantojot skalu "42", mēs varam apli sadalīt 7 daļās, jo 42 tiek dalīts ar 7 bez atlikuma - tas ir 6 dalījums. Attiecīgi ar tās palīdzību jūs varat sadalīt loku 14, 21, 42 daļās. 360 daļu mērogs to nepieļaus.
2. Sadalot priekšējo plāksni 360 daļās, mēs varam sadalīt 2, 3,4,5,6,8,9,10,12,15, 18,20,24,30,36,40,45,60,90,120,180 dalījumu un tikai 21 vērtību.
Universālā skala papildus šīm vērtībām ļaus sadalīt vēl vairākas vērtības: 7, 14, 16, 21, 48, 72, 80, 144, 240. Tas ir, vismaz pie 30 vērtībām.
Līdz ar to universālā skala ir funkcionālāka nekā 360 dalīšanas skala.
2. daļa. Nedaudz par kļūdu teoriju.
Par aksiomu mums jāpieņem, ka jebkurš (!!!) mērījums, ko mēs varam izdarīt tikai ar kļūdu. Vai arī citādi praktiski nav iespējams veikt nekādus mērījumus bez kļūdām.
Mērījumu precizitāti ietekmē vairāki faktori. Mēs uzskaitām dažus no tiem.
1. Jebkurš mērīšanas rīks atšķiras no atsauces.
2. Jebkuram gājienam ir reālas lineāras dimensijas.Piemēram, kompasa adatas galam ir vairāku mikronu "biezums", labi, piemēram, piemēram, 10. Apvienojot lineālu ar šādu gājienu, mēs nevaram "ar aci" noteikt, uz kuru gājiena daļu lineāla mala nokrīt: viena, otrā vai trešā mikrona biezums.
3. Visizcilākā zīmuļa biezums ir arī aptuveni 0,2 mm, turklāt ar katru gājienu šis biezums mainās grafīta nobrāzuma dēļ.
Secinājums: praktiskām vajadzībām 2007 mājās apstākļos, mēs varam "paļauties" uz precizitāti dažu milimetru simtdaļu robežās.
Balstoties uz iepriekšminētajiem apsvērumiem, marķējot pamatni, jāizmanto asākās adatas, plakanie lineāli, glītās rokas un dedzīgā acs.
3. daļa. Marķējums.
Marķēšanai es izgatavoju rāmi no stieņu atgriezumiem, skaidu plātnes gabala. Rāmis tika piestiprināts mašīnai ar skavām, savukārt ekrāna plaknei (kokšķiedru plātnes loksnei ar papīra lapu) jābūt perpendikulārai mašīnas vadotnēm. Un vēl viena prasība: ekrānam jābūt izvietotam ne tikai perpendikulāri, bet arī tā, lai lineāls, kas uzstādīts uz mašīnas patronas ass, slīdētu pāri ekrānam bez spraugas. Šis izkārtojums ir nepieciešams, lai maksimāli novērstu iespējamās iezīmēšanas kļūdas.
Pievērsiet uzmanību tam, ka mūsu ekspromtētais cinka pārklājuma lineāls arī cieši pieguļ pie pamatnes plāksnes, un “darba” daļai (tai daļai, ar kuru mēs izdalīsim risku) vajadzētu būt perpendikulārai plāksnes plāksnei. Tā vietā, lai apcirptu cinkošanu, jūs, protams, varat ņemt metāla lineālu. Bet apdari var viegli saliekt, lai tā cieši piegultu pie pamatnes. Nostiprināts ar kravu. Man ir šis metāla disks.
Līnijai no stūra ir pieci caurumi, kas visi atrodas uz vienas līnijas. Viens caurums ar diametru 5,8 mm. Tajā ievieto 6 mm matadatu, kuru abās pusēs piestiprina ar uzgriežņiem. Šādus 4 caurumus es izurbu ar 1 mm urbi, un tie atrodas no pirmā cauruma ass attiecīgi 195 (36 dalījumiem), 220 (60), 241 (42), 260 (48 dalījumiem) mm. No pieredzes teikšu, ka urbis jāuzņem divreiz plānāks - 0,4 - 0,5 mm. Bet man tā nebija pa rokai. Fakts ir tāds, ka šajos caurumos mēs ievietosim asinātu zīmuli, un, pagriežot lineālu, mēs ievilksim attiecīgā rādiusa loka. Zīmuļa gals caurumā ar diametru 1 mm nedaudz karājas, t.i. rādiuss tiek novilkts ar nelielu kļūdu - 2-3 desmiti.
Atbrīvojot ārējo uzgriezni, lineāls "atslābst" uz balsta. Man ir padota šī dēļa gabals man zem rokas. Bet varbūt tikai skrūve.
Nedaudz ģeometrijas.
Tam nepieciešami visi iepriekš uzskaitītie preparāti. Ģeometrijā ir šāds jēdziens - vienādmalu trīsstūris. Šī ir ģeometriska figūra, kurai ir vienādas malas un attiecīgi vienādi leņķi starp tām, tas ir, 60 grādi. Mūsu gadījumā leņķa virsotne būs mašīnas vārpstas ass, “materializējusies” iesprausta 6 mm matadata formā, uz kuras ir piestiprināts lineāls no alumīnija stūra. Tāpēc trīsstūris atrodas tā pusē. Mēs uzzīmējam tā pamatni uz ekrāna akorda veidā starp serifiem uz atbilstošā loka.
Kā to izdarīt?
Izmantojot asinātu zīmuli un novājinātā lineāla otro, trešo, ceturto un piekto caurumu, mēs zīmējam uz loka papīra lapas.
Pēc tam izmēriet 260 mm no ārējā loka apakšējā punkta, iegūstot vienādmalu trīsstūra pamatnes otro (augšējo) punktu.
Kāpēc uz ārējā loka? Tas ir iespējams uz jebkura no tiem, bet, jo lielāks ir rādiuss, jo precīzāk mēs varam atzīmēt un uzzīmēt akordu - trīsstūra pamatni. Faktiski nav nepieciešams novilkt pamatlīniju: līknē izmantosim tikai serifus, kas ir trijstūra sānu leņķu virsotnes - leņķi pie tās pamatnes.
Šo vienādmalu trīsstūra īpašību mēs varam izmantot šādi: mūsu lineāls no stūra, nolaists uz leju līdz atbalstam, ir izlīdzināts ar vienu trīsstūra pamatnes punktu. Tad mēs piestiprinām lineālu ar atslēgu, pievelkot uzgriezni. Mēs riskējam uz plāksnītes, uz skotu lentes uzrakstām pirmo atzīmi - "O". Pagrieziet kārtridžu ar roku, līdz lineāls ir izlīdzināts ar trīsstūra pamatnes otro punktu.
Tādējādi priekšējā plāksne tika pagriezta par 60 grādiem. Ar adatu uz plāksnītes mēs izgatavojam marķējumu, un uz lentes mēs rakstām, ka tas ir "60".
Tad novājiniet uzgriezni, kas nostiprina lineālu, lineāls iet uz leju, "līdz pamatnei", nepieskaroties kārtridžam. Tas ir, lineālu atkal izlīdzina ar trīsstūra pamatnes pirmo punktu. Nostipriniet uzgriezni, liedzot lineāram mobilitāti. Grieziet patronu ar roku, līdz lineāls ir izlīdzināts ar trīsstūra pamatnes otro (augšējo) punktu. Mēs riskējam uz plāksnītes, uz lentes rakstām, ka tas ir "120". Un tā tālāk, izmantojot to pašu algoritmu, marķējiet virsmu ar etiķetēm “180”, “240” un “300”.
Tā rezultātā mēs iegūstam iespēju sadalīt loku 2, 3 un 6 daļās.
Pārvietojamies tālāk. Mums ir jāsaņem riski uz plāksnītes ar 30 grādu dalījumu. Lai to izdarītu, trīsstūra pamatne jāsadala uz pusēm. Rezultātā lineāla rotācijas leņķis no apakšējā punkta līdz jaunam punktam pamatnes vidū būs 30 grādi. Ir divi veidi, kā sadalīt trīsstūra pamatni. Pirmais. Mēs ņemam lineālu, un no pamatnes apakšējā punkta mēs atlikām 130 mm, tas ir, uz pusi no pamatnes (akordi) garuma.
Otrais ir ģeometrisks. Mēs uzņemam kompasu, un ar tā palīdzību, izkliedējuši kājas garumā, kas pārsniedz pusi no pamatnes garuma (manā piemērā, apmēram 150-160 mm), mēs streikojam uz vienu un otru pamatnes pusi, pārklājoties ar ierosināto sektoru ar pusi no pamatnes garuma. Tad mēs pārkārtojam kompasa adatu trīsstūra augšpusē, nemainot attālumu starp kompasa kājām, un veicam tos pašus riskus, kuriem vajadzētu pārklāties ar iepriekš ievilktajiem. Mēs savienojam iegūtos punktus, un šīs līnijas krustojumā ar trīsstūra pamatlīniju būs puse no šīs pamatnes garuma.
Un tagad, izmantojot to pašu algoritmu, mēs sadalām priekšējo plāksni, izraisot sadalījumu līdz 30 grādiem. Lai to izdarītu, apvienojiet jebkuru no iepriekš piemērotajiem modeļiem ar augšējā lineāla malu. Novājiniet uzgriezni, nolaidiet lineālu līdz apakšējam punktam. Mēs nofiksējam uzgriezni, pagrieziet virpas patronu līdz jaunai atzīmei - 30 grādi. Mēs riskējam, uz skotijas lentes uzrakstām atbilstošo etiķeti. Piemēram, ja tiek kombinēts “120” risks, tad, pagriežot kasetni vienā virzienā pulksteņrādītāja virzienā, mēs iegūstam atzīmi 150 grādi. Un, pagriežot to pretēji pulksteņa rādītāja virzienam, jūs saņemat 90 grādus. Un tā tālāk visiem iepriekš saņemtajiem riskiem (atzīmēm), līdz priekšējā plāksne ir pilnībā piepildīta ar atzīmēm ar 30 grādu dalījumu.
Rezultātā mēs iegūstam iespēju sadalīt loku vairākās vērtībās: 4, 8 un 12 daļās.
Tagad, lai pabeigtu galvenās skalas dalījumu piemērošanu, jums jāpiemēro dalījums ar cenu 15 grādi. Tas ir, 30 grādu sektori jebkurā veidā jāsamazina uz pusi. Mēs jau to pārzinājām tādā nozīmē, ka mēs to izdarījām 60 grādu sektoriem. Tātad uz ekrāna mēs iegūstam atzīmes ar 15 grādu dalījumu, un ar viņu palīdzību mēs riskējam uz plāksnītes.
Tātad galvenā skala ir gatava, tas ir, skala ar dalījumiem par cenu 15 grādi.
Tagad jums ir jāpiemēro vēl 4 skalas šai galvenajai skalai, lai sadalītu 60, 48, 42 un 36 dalījumos. Grafiski tas izskatās šādi:
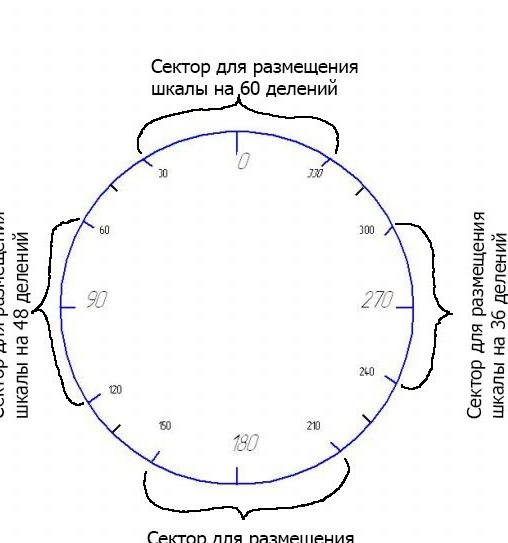
Es svarus ievietoju šādā secībā. Bet jūs varat ievietot jebkuru no šīm svariem jebkurā citā vietā pēc saviem ieskatiem. Šis izvietojums man šķita ērtāks. Lūdzu, ņemiet vērā, ka starp svariem palika neskarti sektori 30 grādu leņķī. Jūs varat, protams, paplašināt mēroga sektorus, jo ir atlikušie brīvie sektori. Es to nedarīju, lai nepārslogotu svarus. Piemēram, 42 dalījumu skalai 5 iegriezumus pie 8.57 ar risku 180 jebkurā virzienā “aizsargā” 42,85 grādi. Tas ir, gandrīz tuvu atzīmēm 135 vai 245, kas var sarežģīt to izmantošanu.
4. daļa. 60 dalījuma skalas rasējums.
Lai sadalītu šo mērogu, mums jāsaņem dalījumi, kuru cena ir 6 grādi. Lai to izdarītu, atkal nedaudz ģeometrijas. Lai iegūtu trijstūri aplī ar leņķi 6 grādu augšpusē, mums jāaprēķina šāda trīsstūra pamatnes garums. Trijstūris būs vienādmalu, un apļa trijstūra pamatne ir akords.
Akorda aprēķināšanas formula ir šāda: L = 2 * R * sin (A / 2), L ir akorda garums, R ir apļa rādiuss, A ir leņķis.
No visiem mums zināmajiem daudzumiem mēs zinām tikai leņķa vērtību - 6 grādi. Puses sinusa atrašana no 6 grādiem ir tehnoloģijas jautājums.
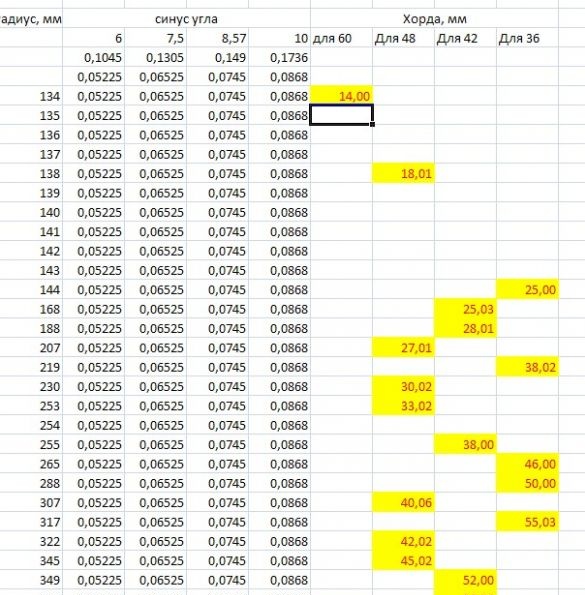
Es to izdarīju vēlāk: es izmantoju "zinātniskā kule" metodi. Izmantojot programmu Excel, tabulu, kurā es iekļāvu rādiusa garumus ar gradāciju caur 1 mm, sākot no 130. Un pēc formulas es ieguvu akorda garuma vērtības. Tabula izrādījās gara, daļa no šīs tabulas pēc nevajadzīgu vērtību (daļēja) izdzēšanas izskatījās šādi:
Atliek izvēlēties vēlamās vērtības. Tā kā aprēķini tika veikti ar precizitāti līdz 0.00001, es, pirmkārt, izvēlējos pat vērtības, kas dalāmas ar 4. Otrkārt, tās, kuras varēja noapaļot, ja pēc komata nebūtu vairāk par 0,03. Šis ir jautājums par kļūdām: mēs nevaram “izsekot” trīs simtdaļas, ja izmantojam svarus. Atgādināšu, ka zīmuļa līnijas biezums ir vismaz 0,2 mm. Tātad simtdaļas var droši atstāt novārtā (mēs jau esam pieraduši, ka mērījumos vienmēr ir kļūdas).
Kāpēc ir nepieciešams "dalīt" ar 4? Bet vienkārši. Galu galā vispirms trīsstūra pamatni sadalījām ar 2, bet pēc tam vēlreiz ar 2. Un rezultātā mēs ieguvām skaitli, kas nav dalīts.
Vērtību atlase izskatījās šādi:
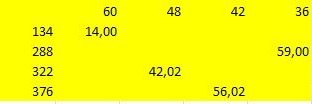
Bet tad es atteicos no šīs izvēles, jo starp 134 un 376 mm plaisa ir pārāk liela. Un meklēja citas nozīmes. To atradu. Viņi vairs nav tabulā, jo Es tos izgriezu. Šīs vērtības ir 195,220,241 un 260 mm. Loki ar šādiem rādiusiem ir izvietoti diezgan kompakti, netraucējot viens otram. Jā, ne visi ir dalāmi ar 4 bez atlikuma. Un mums nav vajadzīgs viss. Lai izveidotu galveno skalu, es paņēmu loka ar lielāko rādiusu. Lai sadalītu uz pusēm, es izmantoju grafisko metodi, t.i. izmantojot kompasu. Un, ja jūs nolemjat izmantot lineālu, - karodziņu jūsu rokās !, - mērogu ar rādiusu 260 mm sadala divreiz uz pusēm bez atlikušās daļas. Akordu garums ir attiecīgi 34, 23, 36 un 34 mm.
Tātad nozarē, kas paredzēta sadalīšanai 60 dalījumos, ir jāpiemēro riski ar dalīšanas cenu 6 grādi. Kā to izdarīt? Viss ir vienkārši, piemēram, tvaika lokomotīves pīkstiens. Izmantojot lineālu vai kompasu, mēs atlikt 23 mm hordu no apakšējā vai jebkura cita loka loka, kura rādiuss ir 220 mm. Virsmas plāksnes risks ar vērtību "90" tiek apvienots ar augšējā lineāla malu. Mēs apvienojam apakšējo lineālu ar iegūtā akorda vienu galu, piestipriniet uzgriezni, saspraudiet lineālu. Mēs pagriežam kārtridžu, lai izlīdzinātu lineāla malu ar akorda otro galu. Ieguva 6 grādu leņķi. Ar kompasa adatu mēs riskējam uz plāksnītes. Lai paātrinātu procesu (un vismaz nedaudz samazinātu mērījumu kļūdu skaitu), labāk ir izmantot kompasu, lai izveidotu serifus nevis vienam akordam, bet vairākiem. Tad nevajadzēs katru reizi atskrūvēt uzgriezni, izlīdzināt lineālu ar apakšējo punktu, bet vienkārši pēc nākamo risku pielietošanas mēs pagriežam kārtridžu līdz nākamajiem riskiem (nākamā horda beigām).
5. daļa. Atlikušie svari.
Akorda garums 36 dalījumu skalai ir 34 mm, ko mēs, tāpat kā iepriekš, atzīmējam uz loka, bet ar rādiusu 195 mm. Ja jūs “veidojat” 6 šādus akordus, tad jūs varat sākt atzīmēt skalu ar vērtību “240” un beigties ar vērtību “300”. Viena dalījuma cena ir 10 grādi.
Un tālāk, saskaņā ar pārbaudīto algoritmu, izmantojot 260 mm loku, skalu sadala 48 dalījumos (akorda garums ir 34 mm). Dalīšanas cena ir 7,5 grādi.
Izmantojot 241 mm loku, skalu sadala 42 dalījumos. Akorda garums ir 36 mm, dalīšanas cena ir 8,57 grādi.
Secinājums
Vēlreiz par jautājumu: kāpēc tas tik ļoti sarežģī marķējumu? Atbilde ir vienkārša: nevajag tevi, nevajag. Man bija vajadzīgs šāds sadalījums, lai nākotnē varētu veikt pārnesumus ar zobiem 42 un 48 zobiem. Joprojām ir nepieciešami svari 29 un 32 zobiem. Bet es tos padarīšu jau pieejamus, izmantojot īslaicīgu lentes sadalījumu. Bet tas būs vēlāk.
Un pēdējais jautājums: kā to izmantot, jo katrs no svariem (izņemot galveno) ir īss, viss segments ir 1/6 no plāksnes apkārtmēra?
Atbilde: ērti lietojama. Es parādīšu nedaudz vēlāk video (kad to uzstādīšu). Pa to laiku īsi pastāstiet.
Uz kasetnes jums jāpielīmē lente. Viena vietā jums jāņem divi labākie valdnieki. Tas ir labāk no cinkošanas, lai lineālu varētu viegli saliekt.
Un tagad pāris piemēri. Teiksim, ka mums ir jāiezīmē aplis 6 daļās. Lai to izdarītu, izmantojiet galveno skalu ar vienu augšējo lineālu. Konsekventi apvienojot 0, 60, 120, 180, 240 un 300 riskus, mēs iegūstam dalījumu 6 daļās. Aplis, ēst, bet ir iespiests kārtridžā, kuru mēs pagriežam un riskējam gar griezēja malu vai pats griezējs.
Tagad atzīmējiet apli, kas iespīlēts kārtridžā, 5 daļās. Galvenajā skalā šādu dalījumu nav.Tad domāsim, kura no skalām dalāma ar 5 bez atlikušās daļas? Patiesība: 60 bāru skala. Tie ir 12 iedalījumi. Bet sasodīts: mums mērogā ir tikai 10 dalījumi !?
Mierīgi, bez panikas. Vienas šādas skalas dalīšanas cena ir 6 grādi. Tāpēc 12 dalījumi ir 72 grādi. Un galvenajā skalā iepriekšējā piemērā mēs izmantojām 60 grādu sektorus. Un kas mums traucē apvienot vienu augšējo līniju ar "300" risku, bet otru - apvienot otrajā riskā pa kreisi no "0". Tas ir, pievienojiet 60 reizes 2 reizes līdz 6, mēs iegūstam 72. Mēs novietojam lineālus tā, lai tie cieši piegultu pie pamatnes. Vai tas nedarbojas? Ir taisnība, ka priekšējās plāksnes rādiuss ir pārāk mazs, izliekums ir liels, un lineāli vai nu karājas gaisā, vai arī tie būs saliekti tā, lai tie cieši piegultu pie seguma plāksnes. Neveiciet ne vienu, ne otru. Vienkārši pagrieziet galvu, un 12 dalījumu vietā ņemsim 6 dalījumus, t.i. 36 grādi. Un mēs kļūstam par valdniekiem caur 6 dalījumiem.
Uz lentes ar zīmuli vai pildspalvu mēs uz lineāliem zīmēsim svītras. Uz mūsu apļa mēs izveidojam pirmo iecirtumu ar griezēju. Mēs pagriežam kārtridžu ar rokām, teiksim, pulksteņa laikā, līdz līmlentes kreisais gājiens ir izlīdzināts ar labā lineāla malu. Mēs pagriezāmies par 36 grādiem. Uz lentes kreisajā lineālā mēs riskējam un pagriežam kārtridžu uz šo risku. Tātad mēs pagriezāmies par 72 grādiem. Mēs izveidojam otro iecirtumu ar griezēju. Un tā tālāk. Viens smalkums. Zīmes ar pildspalvu vai zīmuli ir “biezas” neatkarīgi no tā, cik smagi mēģināt. Tāpēc labā lineāla mala, pagriežot kārtridžu, nav jāapvieno ar kreisās līnijas labo malu, bet ar tās kreiso malu. Tas ir, gandrīz pilnībā līnijai vajadzētu iet zem labā lineāla. Pretējā gadījumā ar katru mērījumu uzkrājas kļūda 2-3 desmiti. Un aplī tas var būt vairāk par milimetru.
Lai sadalītu 14 daļās, jāizmanto 42 dalījumu skala. 42: 14 = 3 dalījumi.
Interesantāks ir jautājums par sadalījumu, pieņemsim, ka par 144 daļām. Es nezinu, kam tas vajadzīgs, bet pēkšņi? Šeit algoritms ir atšķirīgs. Mums nav svari, kas būtu dalāms ar šo skaitli. Tad mēs meklējam nevis iegriezumu skaitu ar viena dalījuma grādiem. 360: 144 = 2,5 grādi. Kur iegūt 2,5 grādus? Un ja mūsu mērogā? !! Mums ir skala ar dalīšanas cenu 10 grādi. Un tur ir skala ar dalīšanas cenu 7,5 grādi. Ja 10 - 7,5 = 2,5. Šeit ir vēlamais rezultāts! Kā to panākt? Skala 36 tiek nogādāta augšpusē, pie valdītājiem. Mēs apvienojam vienu lineālu ar vienu mēroga risku, otru ar citu, ar tuvāko. Starp valdniekiem mums ir 10 grādu sektors. Tagad mēs pagriežam kārtridžu, novedot lineālu uz skalu līdz 48. Tā dalījumu cena ir 7,5 grādi. Mēs kombinējam vienu mēroga risku, piemēram, ar kreiso lineālu, kuru mēs nepieskārām. Tad mēs pārvietojam šo lineālu uz otro, līdz tas tiek tuvināts ar tuvāko skalas risku par 48. Tas ir, mēs samazinām 10 grādu sektoru par 7,5. Atlikušajā daļā starp valdniekiem mēs iegūstam 2,5 grādu sektoru. Un ej! Pēc tāda paša principa kā sadalot 5 daļās, mēs izmantojam divus lineālus.
Labi, vēl viens piemērs. Pieņemsim, ka vēlaties sadalīt apli 40 daļās. Skaitīts: 360: 40 = 9 grādi. Raudāja - mums nav tāda mēroga! Ieslēdziet galvu. Mums ir skala ar dalīšanas cenu 7,5 grādi. Divas šīs skalas iedaļas veidos 15 grādu sektoru. Novietojiet lineālus attālumā viens no otra divās daļās ar skalu 48.
Un tagad no 15 jums ir jāatņem 6, lai iegūtu vēlamos 9 grādus. Kur mums ir 6? Tieši tā, skalā 60. Mēs jau zinām, kā ar valdnieku palīdzību veikt dažus grādus. Mēs darām, iezīmējam.
Izmantojot to pašu principu, loku var sadalīt 80 daļās. 360: 80 = 4,5 grādi. Trīs dalījumi skalā 48 dos 3 x 7,5 = 22,5. Trīs dalījumi skalā 60 sniegs 3 x 6 = 18 grādus. 22,5 - 18 = 4,5.
Un atkal pie kļūdu teorijas. Ja jūs apļāvāt lielu skaitu rakstu, kļūda tiek uzkrāta pie katras atzīmes. Lai samazinātu kļūdu, es iesaku izdarīt pusi atzīmju. Un tad atgriezieties sākumā un veiciet marķēšanu otrā virzienā, arī uz pusi. Kad šīs "pusi" zīmes saplūst (un tās gandrīz nekad nesaskaņo), tad mēs redzēsim uzkrāto kļūdu apmēru. Piemēram, sadalot 8 daļās, es parādīju marķējuma kļūdu aptuveni 0,1 - 0,2 mm. Vītņotiem savienojumiem tas nav kritiski: skrūvju vītnes vienmēr tiek sabojātas par 3-4 desmitiem. Bet, ja es turpinātu ar iezīmēšanu secīgi, tad kļūdas lielums varētu palielināties līdz 0,5 mm, un tas jau ir daudz.Secinājums no lielu skaitļu teorijas: jo mazāk mērījumu veicam, jo mazāk kļūdāmies. Un otrādi: jo vairāk mērījumu, jo vairāk kļūdu uzkrājas. Tas ir jāņem vērā.